Hijo de un vizconde, Bertrand Russell nació en Monmouthshire (Gales) en 1872. Estudió filosofía y matemáticas en la Universidad de Cambridge, de donde fue expulsado de un puesto docente en 1916 por actividades antibélicas. Destacado pacifista y crítico social, en 1918 pasó seis meses en prisión, en los que escribió Introducción a la filosofía matemática.
Russell enseñó en EE UU en la década de 1930, aunque su nombramiento en una universidad de Nueva York fue revocado debido a una declaración judicial que cuestionaba su moralidad. Recibió el premio Nobel de Literatura en 1950, y en 1955 publicó con Albert Einstein un manifiesto llamando a la prohibición de las armas nucleares. Más adelante se opuso a la guerra de Vietnam. Russell murió en 1970.
La lógica en las matemáticas
La idea extendida de unas matemáticas lógicas, con reglas fijas, evolucionó a lo largo de milenios, remontándose a la antigua Grecia y la obra de Platón, Aristóteles y Euclides. En el siglo XIX, una definición rigurosa de las leyes de la aritmética y la geometría surgió en la obra de George Boole, Gottlob Frege, Georg Cantor, Giuseppe Peano y, en 1899, Grundlagen der Geometrie (Fundamentos de la geometría), de David Hilbert. En 1903, Bertrand Russell publicó Los principios de la matemática, donde revelaba un fallo en la lógica de una de las áreas de la matemática. En el libro exploraba una paradoja, conocida como paradoja de Russell (o paradoja RussellZermelo, en referencia al matemático alemán Ernst Zermelo, autor de un descubrimiento similar en 1899).
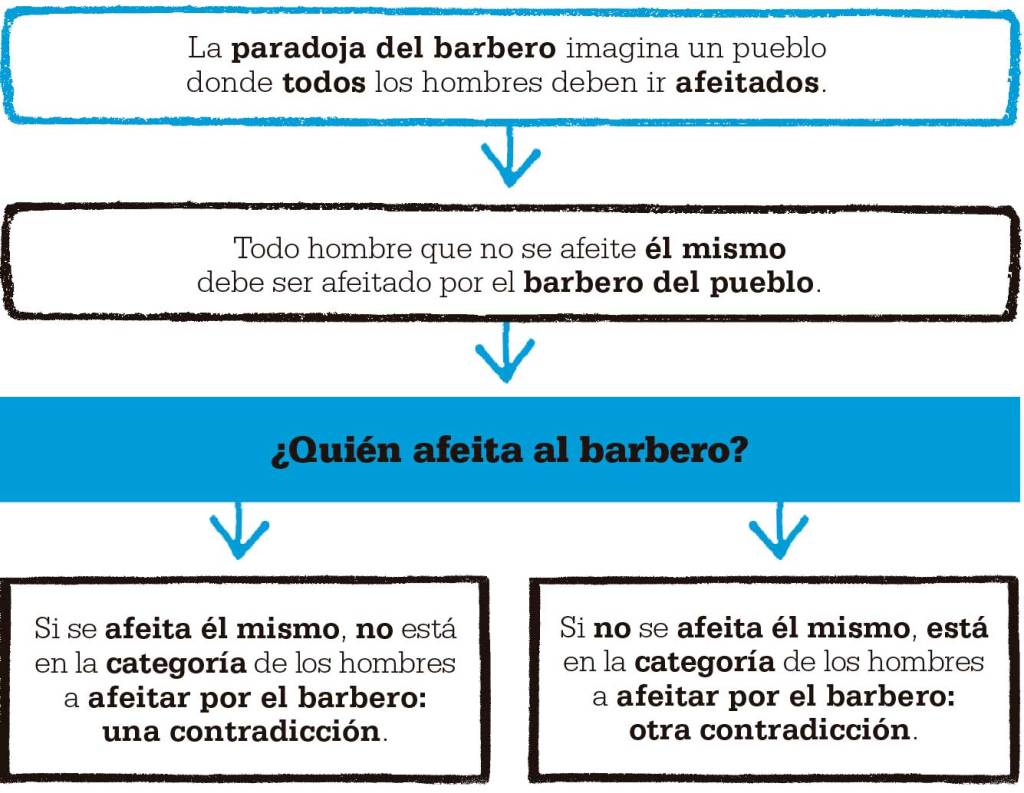
La paradoja implicaba que la teoría de conjuntos, que se ocupa de las propiedades de los conjuntos de números o funciones, y que se estaba convirtiendo rápidamente en fundamento de las matemáticas, contenía una contradicción. Para explicar el problema, Russell empleó la analogía de un barbero, en la que este afeita a todos los hombres de un pueblo salvo a los que se afeitan ellos mismos. Esto crea dos conjuntos, el de los que se afeitan a sí mismos y el de los que afeita el barbero, y también plantea la pregunta: si el barbero se afeita a sí mismo, ¿a cuál de los dos conjuntos pertenece? La paradoja del barbero de Russell contradecía lo dicho por Frege en Grundgesetze der Arithmetik (Leyes básicas de la aritmética) en cuanto a la lógica de las matemáticas, lo cual señaló Russell a Frege en una carta en 1902. Frege se declaró anonadado, y no encontró nunca una solución adecuada.
Una teoría de tipos
Russell procedió entonces a ofrecer su propia respuesta, desarrollando una teoría de tipos lógicos que ponía restricciones al modelo establecido de la teoría de conjuntos (la teoría ingenua de conjuntos), y creaba una jerarquía, de modo que el «conjunto de todos los conjuntos» recibía un trato distinto al de sus conjuntos menores constituyentes. Russell evitó por completo la paradoja, dando un rodeo. Aplicó los nuevos principios lógicos en el imponente Principia mathematica, escrito con Alfred North Whitehead y publicado en tres volúmenes entre 1910 y 1913.
Vacíos lógicos
En 1931, el matemático y filósofo austriaco Kurt Gödel publicó sus teoremas de la incompletitud (continuación del teorema de la completitud de unos años antes), en el que concluía que siempre existirán enunciados sobre los números que pueden ser verdaderos, pero no se podrán demostrar. Además, ampliar las matemáticas añadiendo simplemente nuevos axiomas arrojará nuevas «incompletitudes». En otras palabras, los empeños de Russell, Hilbert, Frege y Peano por desarrollar un marco lógico completo, por riguroso que se intentase hacer, estaban destinados a tener vacíos lógicos.
El teorema de Gödel implicaba también que algunos teoremas matemáticos no demostrados todavía, como, por ejemplo, la conjetura de Goldbach, podrían no demostrarse nunca. Sin embargo, esto no ha disuadido a los matemáticos de realizar decididos esfuerzos por desmentir a Gödel.
El texto y las imágenes de esta entrada son un fragmento de: “El libro de las matemáticas”
