Uno de los conceptos matemáticos fundamentales del siglo XVII fue desarrollado independientemente por dos gigantes científicos de la época, el alemán Gottfried Leibniz y el inglés Isaac Newton.
Construyendo sobre el trabajo llevado a cabo por Gilles de Roberval para hallar el área bajo una cicloide, Leibniz y Newton trabajaron sobre el cálculo de fenómenos como el cambio continuo y la aceleración, que venían desconcertando a los matemáticos desde que Zenón de Elea expusiera sus famosas paradojas del movimiento en la antigua Grecia. La solución a la que llegaron Leibniz y Newton fue el teorema fundamental del cálculo, un conjunto de reglas para calcular con infinitesimales. Para Newton, el cálculo era una herramienta práctica para su trabajo en física, sobre todo aquel relacionado con el movimiento de los planetas; Leibniz, por el contrario, reconoció su importancia teórica, y refinó las reglas de la diferenciación y la integración.

- Figuras clave: Isaac Newton (1642–1727), Gottfried Leibniz (1646–1716)
- Antes:
- 287–212 A.C. Arquímedes aplica el método exhaustivo al cálculo de áreas y volúmenes, introduciendo el concepto de los infinitesimales.
- 1630 Pierre de Fermat usa una técnica nueva para hallar tangentes de curvas, localizando los puntos máximo y mínimo.
- Después:
- 1740 Leonhard Euler aplica las ideas del cálculo a la síntesis de cálculo, álgebra compleja y trigonometría.
- 1823 Augustin-Louis Cauchy formaliza el teorema fundamental del cálculo.
Gottfried Leibniz
 Gottfried Leibniz nació en Leipzig (Alemania) en 1646, y se crio en una familia académica. Su padre era profesor de filosofía moral, y su madre, hija de un profesor de derecho. En 1667, después de completar sus estudios universitarios, Leibniz fue consejero legal y político del elector de Maguncia, lo cual le permitió viajar y conocer a otros estudiosos europeos. Después de morir su patrón en 1673, fue bibliotecario del duque de Brunswick en Hannover.
Gottfried Leibniz nació en Leipzig (Alemania) en 1646, y se crio en una familia académica. Su padre era profesor de filosofía moral, y su madre, hija de un profesor de derecho. En 1667, después de completar sus estudios universitarios, Leibniz fue consejero legal y político del elector de Maguncia, lo cual le permitió viajar y conocer a otros estudiosos europeos. Después de morir su patrón en 1673, fue bibliotecario del duque de Brunswick en Hannover.
Leibniz fue conocido como filósofo además de como matemático. Nunca se casó y apenas se le honró después de su muerte en 1716. Sus éxitos estaban ensombrecidos por la disputa con Newton por la prioridad en descubrir el cálculo, y no se le reconocieron hasta varios años más tarde.
Isaac Newton
 Isaac Newton nació el día de Navidad de 1642 en Lincolnshire (Inglaterra), y fue criado en su primera infancia por su abuela. Estudió en el Trinity College de Cambridge, donde le fascinaron la ciencia y la filosofía. Durante la epidemia de peste en Londres de 1665–1666, la universidad tuvo que cerrar, y fue entonces cuando formuló sus ideas sobre fluxiones (tasas de cambio en un momento determinado).
Isaac Newton nació el día de Navidad de 1642 en Lincolnshire (Inglaterra), y fue criado en su primera infancia por su abuela. Estudió en el Trinity College de Cambridge, donde le fascinaron la ciencia y la filosofía. Durante la epidemia de peste en Londres de 1665–1666, la universidad tuvo que cerrar, y fue entonces cuando formuló sus ideas sobre fluxiones (tasas de cambio en un momento determinado).
Newton hizo descubrimientos importantes en los campos de la gravitación, el movimiento y la óptica, en los que mantuvo una notoria rivalidad con el eminente científico Robert Hooke. Uno de los puestos gubernamentales que ocupó fue el de maestre de la Real Casa de la Moneda, desde el cual supervisó el cambio del patrón plata al patrón oro. Fue también presidente de la Royal Society. Newton murió en 1727.
El teorema fundamental del cálculo

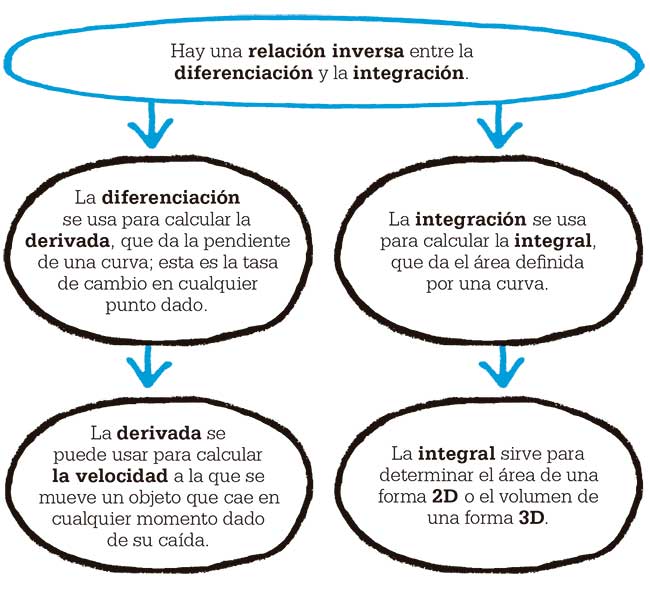
El estudio del cálculo se sustenta en el teorema fundamental del cálculo, que especifica la relación que hay entre la diferenciación y la integración, dependientes del concepto de los infinitesimales. Fue articulado por primera vez en 1668 por James Gregory en Geometriae pars universalis (La parte universal de la geometría); Isaac Barrow lo generalizó dos años después, y Augustin-Louis Cauchy lo formalizó en 1823.
El teorema tiene dos partes. La primera enuncia que la integración y la diferenciación son opuestas: para toda función continua (que se puede definir para todos los valores), existe una «antiderivada» (o integral), cuya derivada (medida de la tasa de cambio) es la función misma. La segunda parte establece que si se insertan valores en la antiderivada F(x), el resultado –la integral definida de la función f(x)– permite calcular áreas bajo la curva de la función f(x).
El cálculo
El desarrollo del cálculo, la rama de las matemáticas que se ocupa de cómo las cosas cambian, fue uno de los progresos más decisivos en la historia de las matemáticas. El cálculo puede mostrar, por ejemplo, cómo cambia la posición de un vehículo a lo largo del tiempo, cómo pierde brillo una fuente de luz a medida que se va alejando o cómo se altera la posición de los ojos de una persona que observe un objeto en movimiento. Puede determinar dónde alcanzan los fenómenos cambiantes sus valores máximo y mínimo, y la velocidad a la que pasan de uno a otro.
Además de las tasas de cambio, otro aspecto importante del cálculo son los sumatorios, que surgieron de la necesidad de calcular áreas. Con el tiempo, el estudio de áreas y volúmenes se formalizó en lo que se conoce como integración, mientras que el cálculo de las tasas de cambio se llamó diferenciación.
Al permitir conocer mejor el comportamiento de los fenómenos, el cálculo sirve para predecir su estado futuro e influir en el mismo. De manera análoga al álgebra y a la aritmética como herramientas para trabajar con cantidades numéricas o generalizadas, el cálculo tiene sus propias reglas, notaciones y aplicaciones, y su desarrollo entre los siglos XVII y XIX condujo al progreso rápido de campos como la ingeniería y la física.
Orígenes antiguos

A los antiguos babilonios y egipcios les interesaba en particular la medición. Era de gran importancia para ellos poder calcular las dimensiones de los campos para cultivar y regarlos, así como el volumen de los depósitos de grano. Y esta necesidad les llevó a desarrollar nociones tempranas de áreas y volúmenes, aunque tendieran a darse en forma de ejemplos muy específicos, como uno incluido en el papiro Rhind que consiste en hallar el área de un campo circular con un diámetro de 9 jet (o khet, una antigua medida egipcia de longitud). Las reglas establecidas en el papiro Rhind condujeron en último término a lo que se conocería como cálculo integral más de 3000 años después.
El concepto de infinito es fundamental en el cálculo. En la antigua Grecia, las paradojas del movimiento de Zenón, un conjunto de problemas filosóficos ingeniados por Zenón de Elea en el siglo V a.C., postularon que el movimiento es imposible por haber un número infinito de puntos intermedios en cualquier distancia dada. En torno a 370 a.C., el matemático griego Eudoxo de Cnido propuso un método para calcular el área de una forma llenándola de polígonos idénticos de área conocida, y luego hacer infinitamente menores los polígonos, de modo que su área combinada acabara convergiendo hacia el área real de la forma.
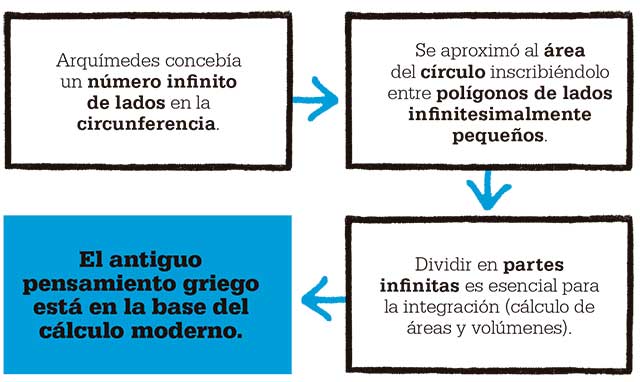
Alrededor de 225 a.C., Arquímedes adoptó este «método exhaustivo» para aproximarse al área de un círculo, inscribiéndolo en un polígono, e inscribiendo otro polígono –ambos con un número cada vez mayor de lados– en el círculo. Cuanto mayor sea el número de lados, más se aproxima el área de los polígonos (de área conocida) a la del círculo. Arquímedes llevó la idea al límite, imaginando un polígono de lados de longitud infinitesimalmente menor. Los infinitesimales fueron un punto de inflexión en el desarrollo del cálculo: problemas hasta entonces irresolubles, tales como las paradojas del movimiento de Zenón, se podían resolver.
Ideas nuevas
Los matemáticos de India y China medievales hicieron nuevos progresos en el manejo de sumas infinitas. También en el mundo islámico, el desarrollo del álgebra permitió el empleo de símbolos generalizados para demostrar que un caso es verdad para todos los números hasta el infinito, en vez de escribir un cálculo millones de veces para todas las variaciones.
Las matemáticas pasaron por una larga época de estancamiento en Europa; sin embargo, en los primeros atisbos del Renacimiento, ya en el siglo XIV, un interés renovado condujo a nuevas ideas acerca del movimiento y las leyes que gobiernan la distancia y la velocidad. El matemático y filósofo francés Nicole Oresme estudió la velocidad de un objeto que se acelera en relación con el tiempo, y llegó a la conclusión de que el área bajo el gráfico que representa esta relación era equivalente a la distancia recorrida por el objeto. Esta idea sería formalizada a finales del siglo XVII por Isaac Newton e Isaac Barrow en Inglaterra, Gottfried Leibniz en Alemania y el matemático escocés James Gregory.
El trabajo llevado a cabo por Oresme se inspiró en el de los calculadores del Merton College de Oxford, grupo de estudiosos del siglo XIV que desarrollaron el teorema de la velocidad media, demostrado después por Oresme. El teorema sostiene que si hay dos cuerpos, uno en movimiento uniformemente acelerado y otro que se mueve a velocidad uniforme igual a la velocidad media del primero, y si la duración del movimiento de ambos es la misma, ambos recorrerán la misma distancia. Los estudiosos del Merton se ocupaban en resolver problemas físicos y filosóficos por medio de cálculos y de la lógica, y les interesaba el análisis cuantitativo de fenómenos como el calor, el color, la luz y la velocidad. Se inspiraron en la trigonometría del astrónomo árabe Al Battani (858–929 d. C.), y en la lógica y la física de Aristóteles.
Nuevos desarrollos
Los pasos progresivos hacia el desarrollo del cálculo se aceleraron a finales del siglo XVI. Alrededor de 1600, el matemático francés François Viète promovió el empleo de símbolos en el álgebra (que hasta ese momento venía utilizando palabras), y el matemático flamenco Simon Stevin inauguró el concepto de límites matemáticos, en el que un sumatorio converge hacia un valor límite, de manera análoga a cómo el área de los polígonos de Arquímedes converge hacia el área de un círculo.
Prácticamente en aquella misma época, el matemático y astrónomo alemán Johannes Kepler estudiaba el movimiento de los planetas, y se propuso calcular el área delimitada por las órbitas planetarias, que reconoció como elípticas y no circulares. Aplicando antiguos métodos griegos, Kepler calculó el área dividiendo la elipse en tiras de ancho infinitesimal.
El método de Kepler, predecesor de la integración más formal aún por llegar, fue desarrollado en 1635 por Bonaventura Cavalieri, matemático italiano, en la obra Geometria indivisibilibus continuorum nova quadam ratione promota (Geometría, avanzada de un modo nuevo por los indivisibles de los continuos), con un método de indivisibles más riguroso para determinar el tamaño de las formas. Hubo nuevos desarrollos en el siglo XVII, con los trabajos del teólogo y matemático inglés Isaac Barrow y el físico italiano Evangelista Torricelli, seguidos de los de Pierre de Fermat y René Descartes, cuyos análisis de curvas promovieron el nuevo campo del álgebra gráfica.
Fermat localizó también los máximos y mínimos, es decir, los valores mayores y menores de una curva (o función).
Modelo de fluxiones
 En 1665–1666, el matemático inglés Isaac Newton desarrolló su método de fluxiones para calcular variables que cambian a lo largo del tiempo, un hito en la historia del cálculo. Como a Kepler y Galileo, a Newton le interesaba el estudio de los cuerpos en movimiento, y buscaba la manera de unificar las leyes que gobiernan el movimiento de los cuerpos celestes y el movimiento sobre la Tierra.
En 1665–1666, el matemático inglés Isaac Newton desarrolló su método de fluxiones para calcular variables que cambian a lo largo del tiempo, un hito en la historia del cálculo. Como a Kepler y Galileo, a Newton le interesaba el estudio de los cuerpos en movimiento, y buscaba la manera de unificar las leyes que gobiernan el movimiento de los cuerpos celestes y el movimiento sobre la Tierra.
En su modelo de fluxión, Newton consideró un punto en movimiento por una curva como dividido en dos componentes perpendiculares (x e y), y luego consideró las velocidades de dichos componentes. Este trabajo puso los cimientos de lo que se conocería como cálculo diferencial (o diferenciación), que junto con el campo relacionado del cálculo integral condujo al teorema fundamental del cálculo.
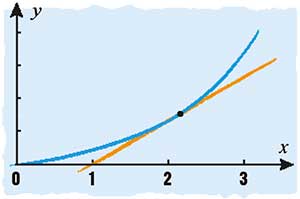
La idea del cálculo diferencial es que la tasa a la que cambia una variable en un punto es igual a la pendiente de una tangente en ese punto. Esto se puede visualizar trazando una tangente (una recta que toca la curva en un solo punto). La inclinación o pendiente de esta recta será la tasa de cambio de la curva en ese punto. Newton reconoció que la pendiente de la curva es cero en los máximos y mínimos, ya que, cuando algo se encuentra en su punto más alto o bajo, momentáneamente, no está cambiando. Newton llevó la teoría más allá al considerar el problema a la inversa: si se conoce la tasa a la que cambia una variable, ¿es posible calcular la forma de la propia variable? Esta «antidiferenciación» suponía calcular el área bajo las curvas.
Newton frente a Leibniz
Mientras Newton desarrollaba el cálculo, el matemático alemán Gottfried Leibniz trabajaba más o menos de manera simultánea en su propia versión, basada en considerar cambios infinitesimales en las dos coordenadas que definen un punto en una curva, o función. Leibniz empleó una notación muy diferente a la de Newton, y en 1684 publicó un trabajo sobre lo que más adelante se conocería como cálculo diferencial. Dos años después publicó otro trabajo sobre integración, de nuevo usando una notación distinta a la de Newton. En un manuscrito inédito fechado el 29 de octubre de 1675, Leibniz fue el primero en usar el signo de la integral ∫, universalmente usado y reconocido en la actualidad.

Fue muy debatida la cuestión de quién descubrió el cálculo moderno, si Newton o Leibniz, y en el amargo enfrentamiento por la prioridad entre los dos se implicó también gran parte de la comunidad matemática. Aunque Newton construyó la teoría de las fluxiones en 1665–1666, no la publicó hasta 1704, cuando fue añadida como apéndice a su Óptica. Leibniz comenzó a trabajar en su versión del cálculo alrededor de 1673, y lo publicó en 1684. Algunos mantienen que los subsiguientes Principia de Newton están influidos por la obra de Leibniz.
Allá por 1712, Leibniz y Newton estaban acusándose abiertamente de plagio el uno al otro. El consenso moderno es que ambos desarrollaron sus ideas sobre la cuestión de forma independiente.
 También fueron importantes las aportaciones de los hermanos suizos Johann y Jacob Bernoulli, y este último acuñó el término «integral» en 1690. El matemático escocés Colin Maclaurin publicó su Treatise on fluxions en 1742, donde promovía y desarrollaba los métodos de Newton y trató de hacerlos más rigurosos. En esta obra, Maclaurin aplica el cálculo al estudio de series infinitas de términos algebraicos. Mientras tanto, el matemático suizo Leonhard Euler, buen amigo de los hijos de Johann Bernoulli, se vio influido por sus ideas sobre el tema. En particular, aplicó la idea de los infinitesimales a lo que se conoce como la función exponencial, ex , lo cual acabó por conducir a la llamada identidad de Euler, eiS + 1 = 0, ecuación que conecta cinco de las cantidades matemáticas más fundamentales (e, i, π, 0, y 1) de un modo muy simple.
También fueron importantes las aportaciones de los hermanos suizos Johann y Jacob Bernoulli, y este último acuñó el término «integral» en 1690. El matemático escocés Colin Maclaurin publicó su Treatise on fluxions en 1742, donde promovía y desarrollaba los métodos de Newton y trató de hacerlos más rigurosos. En esta obra, Maclaurin aplica el cálculo al estudio de series infinitas de términos algebraicos. Mientras tanto, el matemático suizo Leonhard Euler, buen amigo de los hijos de Johann Bernoulli, se vio influido por sus ideas sobre el tema. En particular, aplicó la idea de los infinitesimales a lo que se conoce como la función exponencial, ex , lo cual acabó por conducir a la llamada identidad de Euler, eiS + 1 = 0, ecuación que conecta cinco de las cantidades matemáticas más fundamentales (e, i, π, 0, y 1) de un modo muy simple.
A medida que el siglo XVIII avanzaba, el cálculo resultó cada vez más útil para describir y comprender el mundo físico. En la década de 1750, Euler, en colaboración con el matemático franco-italiano Joseph-Louis Lagrange, usó el cálculo para obtener una ecuación –la ecuación Euler-Lagrange– para comprender la mecánica, tanto de fluidos (gases y líquidos) como de sólidos. A principios del siglo XIX, el físico y matemático francés Pierre-Simon Laplace desarrolló la teoría electromagnética con la ayuda del cálculo.
Formalizar las teorías
 Los diversos desarrollos del cálculo fueron formalizados en 1823, al enunciar Augustin-Louis Cauchy el teorema fundamental del cálculo. En esencia, este sostiene que el proceso de diferenciación (calcular tasas de cambio de una variable representada por una curva) es la inversa del proceso de integración (calcular el área bajo una curva). La formalización de Cauchy permitió considerar el cálculo como un todo unificado, en el que se manejan infinitesimales de una manera coherente, y con una notación universalmente convenida.
Los diversos desarrollos del cálculo fueron formalizados en 1823, al enunciar Augustin-Louis Cauchy el teorema fundamental del cálculo. En esencia, este sostiene que el proceso de diferenciación (calcular tasas de cambio de una variable representada por una curva) es la inversa del proceso de integración (calcular el área bajo una curva). La formalización de Cauchy permitió considerar el cálculo como un todo unificado, en el que se manejan infinitesimales de una manera coherente, y con una notación universalmente convenida.
El campo del cálculo fue objeto de un desarrollo ulterior más avanzado en el siglo XIX. En 1854, el matemático alemán Bernhard Riemann formuló criterios para determinar si las funciones son integrables o no, basados en establecer límites máximo y mínimo para la función.
Aplicaciones omnipresentes
 Numerosos avances de la física y la ingeniería han dependido del cálculo. Albert Einstein lo empleó en sus teorías de la relatividad especial y general a inicios del siglo XX, y ha tenido una aplicación extensa en la mecánica cuántica (que se ocupa del movimiento de las partículas subatómicas). La ecuación diferencial publicada en 1925 por el físico austriaco Erwin Schrödinger trata las partículas como ondas, cuyo estado solo puede determinarse por medio de las probabilidades, algo revolucionario para un mundo científico gobernado hasta entonces por la certeza.
Numerosos avances de la física y la ingeniería han dependido del cálculo. Albert Einstein lo empleó en sus teorías de la relatividad especial y general a inicios del siglo XX, y ha tenido una aplicación extensa en la mecánica cuántica (que se ocupa del movimiento de las partículas subatómicas). La ecuación diferencial publicada en 1925 por el físico austriaco Erwin Schrödinger trata las partículas como ondas, cuyo estado solo puede determinarse por medio de las probabilidades, algo revolucionario para un mundo científico gobernado hasta entonces por la certeza.
El cálculo tiene también numerosas aplicaciones importantes en la actualidad; se utiliza, por ejemplo, en los motores de búsqueda, en proyectos de construcción, estudios médicos, modelos económicos y predicciones del tiempo. Es difícil imaginar un mundo sin esta rama tan ubicua de las matemáticas, entre otras cosas porque sería, casi con certeza, un mundo sin ordenadores. Muchos defenderían que el cálculo es el descubrimiento matemático más importante de los últimos 400 años.
El texto y las imágenes de esta entrada son un fragmento de: “El libro de las matemáticas”
